기초부터 알아가는 CNN

CNN 즉 합성곱신경망은 고수준의 뉴런이 저수준의 뉴런의 출력에 기반한다는 아이디어에서 나온 개념이다.
기존의 완전연결 층에서는 3차원 데이터를 입력 층에 넣어주기위해 1차원 데이터로 변환했다. 이렇게 1차원으로 변환한 데이터는 공간적인 정보가 사라진 상태라 이미지같은 경우 구조가 깨져버려 정보가 많이 사라져버린다. 따라서 구조 정보를 보존하면서 학습하는 방법으로 등장한게 합성곱 신경망 (CNN)이다.
LeCun에 의해 처음 개념이 개발되었고, LeNet이 그 첫번째 구조이다
CNN은 층을 크게 합성곱층(Convolutional Layer)과 풀링층(Pooling Layer)으로 반복하여 구성한다
Convolutional Layers (합성곱층)
합성곱은 3차원 데이터를 필터를 통해 여러 특성을 띄는 채널 (평면)으로 나누는 과정이다.
합성곱층은 매 층마다 모든 픽셀을 연결하는 것이 아니라, 각 뉴런의 수용영역에 있는 픽셀에만 연결이 되기 때문에 처음에는 저수준 특성에 집중하다 점점 고수준 특성으로 조합하게 해준다.
이때 이러한 수용영역이 필터이고, 흔히 생각하는 가중치 파라미터라 할 수 있다고 한다.
합성곱층 연산은 필터를 이동해가면서 데이터에 대응하는 원소끼리 곱한뒤 총합을 구하는 과정인데, 이를 Fused Multiply-Add(FMA)라고 한다. 물론 여기다 Bias 역시 적용될 수 있다.
그림으로 보자면 채널 C에 따라 FN개의 필터(가중치)를 거치면, FN개의 특성을 갖는 데이터가 형성된다.
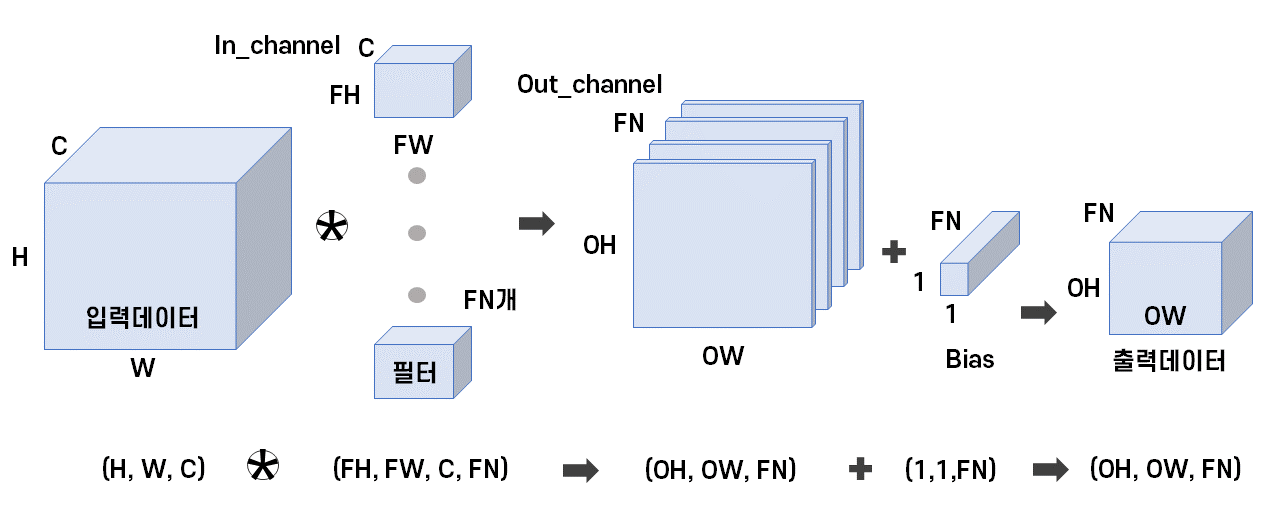
하여튼 이렇게 엄청난 합성 곱 기능을 Pytoch에서 어떻게 사용할까…
Convolution 연산
Pytorch에서 지원하는 Convolution 연산을 위한 레이어들은 Conv1d, Conv2d, Conv3d가 있다.
찾아보기로는 Conv1d는 주로 Text에서 많이 쓴다고 하고, 이미지 분류에는 Conv2d를 주로 사용한다고 한다.
Conv2d는 다음과 같이 구성된다.
Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
in_channels: 입력 채널 수, 흑백은 주로 1 , RGB는 주로 3out_channels: 출력 채널 수kernel_size: 커널 크기stride: stride 크기 즉 입력 데이터에 필터를 적용할때 필터가 이동할 간격. 출력 데이터의 크기를 조절할때 사용. default = 1;padding: 데이터의 크기가 Conv를 지날때마다 작아지는데, 이때 가장자리의 정보가 사라지지 않게 하기 위해서 패딩 사용. 출력이 입력데이터와 공간적인 크기를 동일하게 해주기 위해 default = 0padding_mode: padding을 뭐로 채울껀지, 근데 zero(0) 밖에 지원 안한다고 한다.dilation: 커널 사이 간격groups: 입력 그룹 수 설정 -> 입력 채널을 그룹수로 분류, 출력 그룹 수 설정- > 입력 그룹과 출력 그룹 -> 그 그룹 안에서만 연산bias: bias값을 설정 할지. bias 값은 임계값 같은 느낌으로, input에 가중치를 곱한 네트워크에 더해주는 값이다 (그래프를 좌-우로 움직여줌) default = true;
이제 이미지 Tensor의 Input과 Output에 대해 살펴보자.
Input Tensor (N, C, H, W)
N : 배치의 크기 (몇개인지)
C : 채널 개수 (in_channels)
H : Input Tensor 높이
W : Input Tensor 너비
Output Tensor(N, FN, OH, OW)
N : 배치의 크기 (몇개인지)
FN : 출력 채널 개수 (out_channels)
OH : $\frac{H+2padding[0]-dilation[0]*(kernal_size[0]-1)-1}{stride[0]}+1$
OW : $\frac{H+2padding[1]-dilation[1]*(kernal_size[1]-1)-1}{stride[1]}+1$
Pooling layer (풀링층)
풀링의 이유에는 보통 두가지 이유가 있다고 말한다.
하나는 풀링을 통해 데이터의 크기를 줄일 수 있다. 압축함으로써 처리해야 할 양을 줄일 수 있다.
나머지는 풀링을 통해 추출한 특징들은 이미지 내에서 위치에 변화에 영향을 덜 받는다.
풀링연산이 인접 픽셀들 몇개를 대상으로 진행되어 입력이 조금 변화해도 풀링된 출력들은 거의 변하지 않는데, 따라서 이미지에 있어 위치보다 특징을 더 살피게 만들어 공간적인 한계를 극복한다.
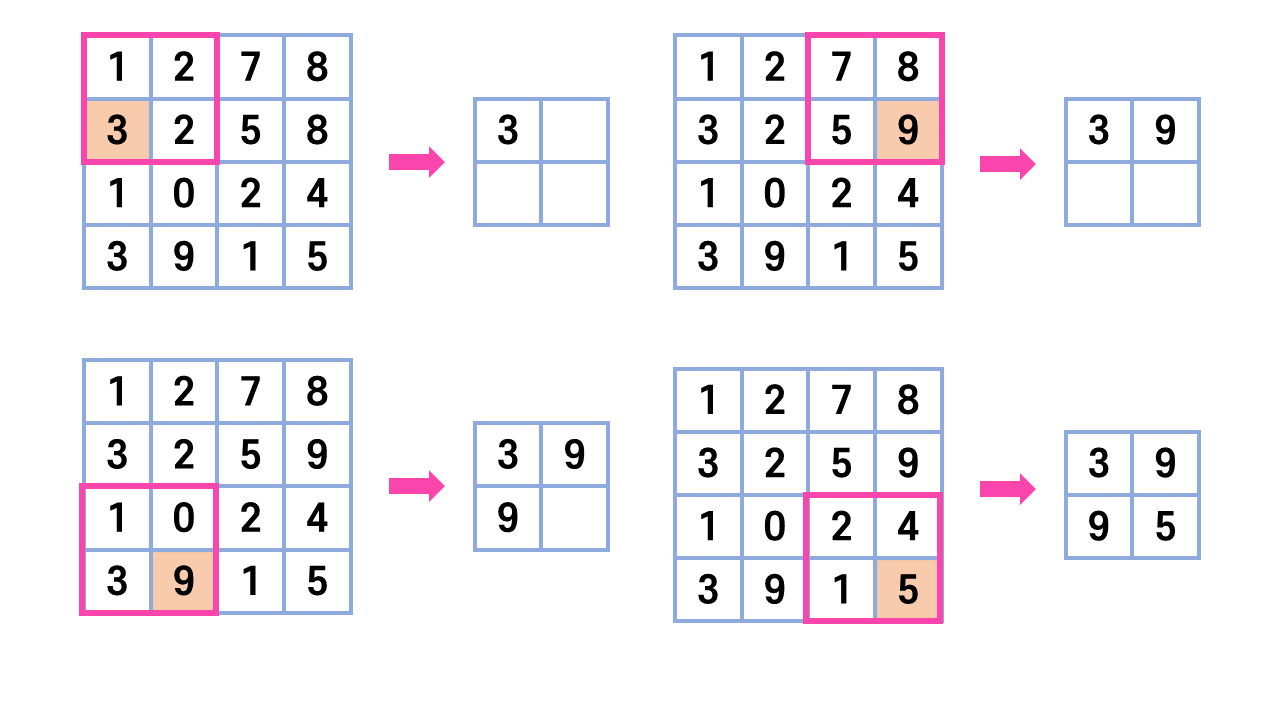
크게 두가지 경우가 있는데 해당 영역에서 최대값을 찾는 MaxPooling과 평균값을 계산하는 AveragePooling이 있다.
Pooling 연산
MaxPool1d, MaxPool2d, MaxPool3d, AvgPool1d, AvgPool2d, AvgPool3d 등이 있는데,
역시 찾아보기로는 주로 이미지에서는 MaxPool2d을 사용한다고 한다.
MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
kernel_size: 커널 크기stride: stride 크기padding: 패딩 크기dilation: 커널 사이 간격return_indices: 최대 인덱스 반환 여부ceil_mode: true면 output 크기를 계산할 때 ceiling 함수 사용
이제 Input과 Output Tensor의 크기에 대해 살펴보자.
Input Tensor (N, C, H, W)
N : 배치의 크기 (몇개인지)
C : 채널 개수
H : Input Tensor 높이
W : Input Tensor 너비
Output Tensor(N, C, OH, OW)
N : 배치의 크기 (몇개인지)
C : 채널 개수
OH : $ \lfloor\frac{H+2padding[0]-dilation[0]*(kernal_size[0]-1)-1}{stride[0]}+1\rfloor$
OW : $ \lfloor\frac{H+2padding[1]-dilation[1]*(kernal_size[1]-1)-1}{stride[1]}+1\rfloor$
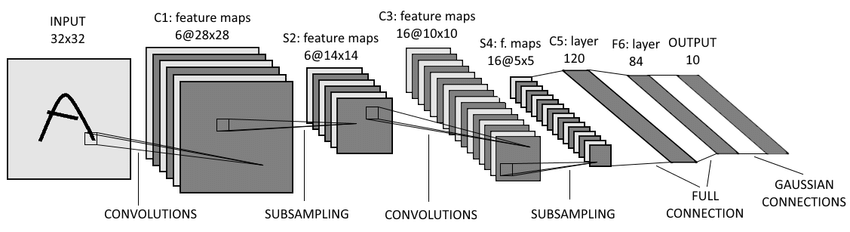
이전 CIFAR-10 연습에서 사용한 LeNet-5모델은 아래와 같이 두번의 Convolution 연산과 두 번의Pooling (SubSampling)연산을 거쳐 특징을 추출한 이후에 Fully-connected 신경망에 보내 분류를 수행하는 것을 알 수 있었다!!
한마디로 CNN은 Convolution과 Pooling을 반복적으로 사용하면서 데이터에서 불변하는 특징을 찾는 과정이다.
이제 이러한 특징을 입력데이터로 Fully-connected 신경망에 보내 분류를 수행하면 된다.
[참고 자료]
https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html https://pytorch.org/docs/stable/generated/torch.nn.MaxPool2d.html https://justkode.kr/deep-learning/pytorch-cnn https://excelsior-cjh.tistory.com/180 https://howtolivelikehuman.tistory.com/96?category=970191
